【论文阅读·ImageDenoising】NBNet:Noise Basis Learning for Image Denoising with Subspace Projection
以下解读均为本人个人见解,如有曲解或造成不必要的麻烦,欢迎联系我 nexisato0810 AT gmail DOT com 进行修改。正文内容中的“作者”均为paper作者本人,我的观点会由“我”或在括号“()”内显式注明。
【Paper作者】:Shen Cheng, Yuanzhi Wang, Haibin Huang. 来自旷视&快手&UESTC团队
【一句话总结】:在UNet中加投影注意力层提升去噪效果
【repo】:https://github.com/megvii-research/NBNet
【Introduction】
以加性噪声为例,图像去噪的主要目的是从有噪声 的图像 中恢复得到一张干净的图像 ,但是由于 $\textbf{x} $ 和 的不确定性,二者是很难被分离开的. 传统的去噪方法NLM、BM3D和小波变换等利用图像和噪声模型的先验知识进行去噪,DNN则是从训练数据中学习到图像的先验和噪声分布. 不过它们依赖于卷积核对图像的局部区域过滤信号和噪声,在信噪比比较低的场景中,没有额外的全局信息就没有那么好用了.
对此,作者团队利用投影的思想:先从输入图像生成一组基向量,将图像投影到一组子空间,再从这些子空间重建回去,可以得到一个高保真的效果.

以U-Net为基础,加入了SSA(Subspace Attention,子空间注意力机制)模块用来学习子空间的基向量和图像的投影. 这个架构在PSNR和SSIM方面实现了SOTA,并且只增加了很少的计算开销.
【相关工作】
- 传统方法:依赖于图像先验知识,包括 NLM、BM3D等,计算复杂度太高,泛化能力不足.
- CNN方法:
- Chen提出TRND模型用于去除高斯噪声;
- DnCNN证实了用DNN去噪时残差学习和BatchNorm的有效性;
- MIRNet提出了通用的图像增强架构用于去噪超分;
- 通过高斯-泊松分布、相机成像模拟、高斯混合模型、GAN等方法合成噪声,在这些数据集上训练的网络同样也具有表现良好的泛化能力.
【网络架构】
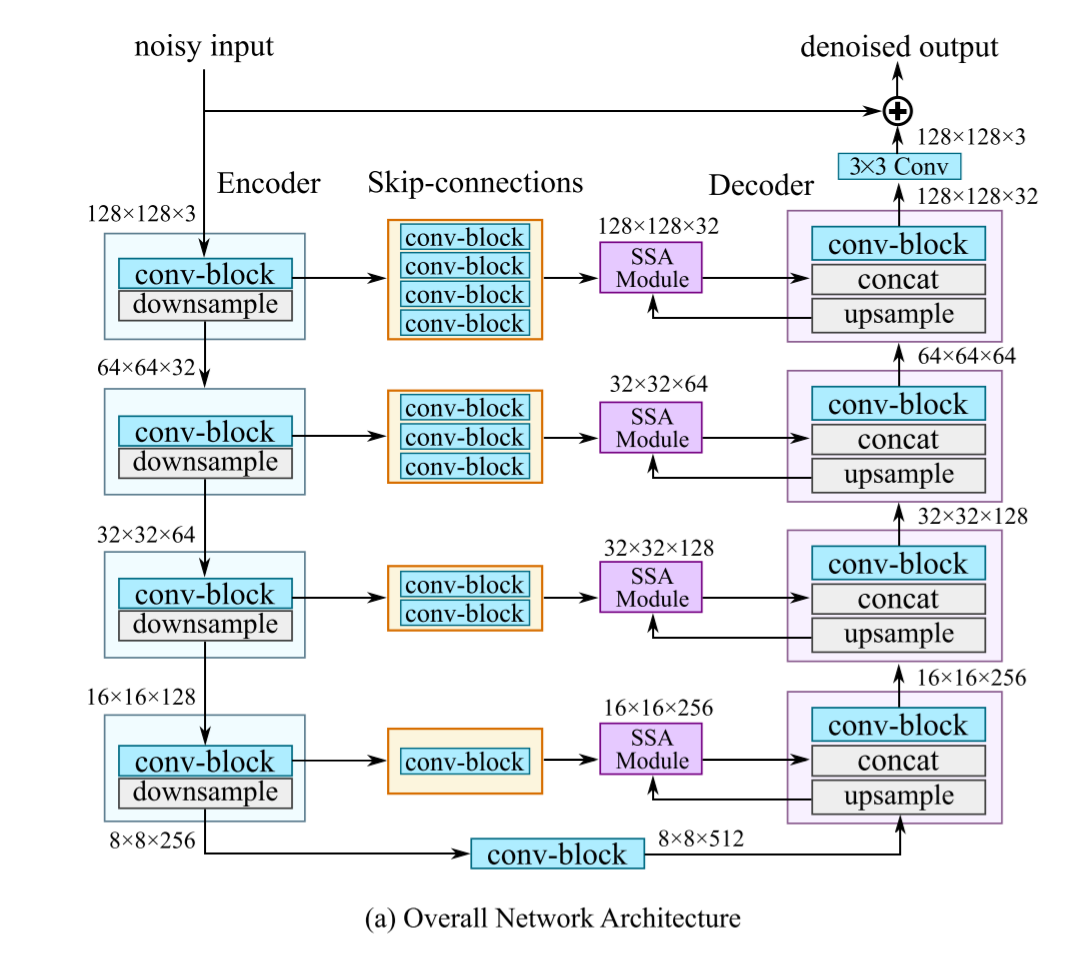
如上图所示,NBNet是一种典型的U-Net风格架构,分别具有4次对称的编解码阶段:
- feature_map在编码阶段每次被降采样到1/2尺度,对应地在解码阶段每次反卷积到2倍的尺度;
- 低层编码块通过跳跃连接层 和 SSA模块 传递给对应的解码块;
- 考虑到低层的feature map含有更多的原始图像特征,因此低层特征 和 高层特征 一块被送入SSA进行计算;也就是说,经过跳跃连接的底层特征 ,在上采样后得到的高层特征图 的引导下,计算得到投影图 ,投影到信号子空间中,然后与原来的高层特征图 级联融合,再经过卷积输出到下一个解码块.
- 最后的输出部分经过一个 3x3 的卷积进行残差计算.
- loss选择L1 loss
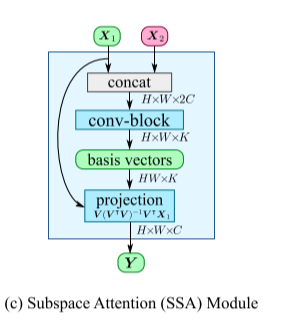
我们比较关注这个SSA模块的设计,一个是子空间的基向量如何生成,一个是如何将特征图投影到信号子空间.
1. 基向量生成
考虑从一张图像上生成的两个feature map ,假设基于这两个feature map有 个基向量 ,其中 .
我们将两个feature map $\textbf{X}_1, \textbf{X}_2 $ 级联得到 , 然后将它送入具有 K层输出通道 的浅层残差卷积块,得到输出维度为 的基向量矩阵 ,卷积块的权重和偏置随着训练不断更新.
2. 投影
的每一个列向量 都是这个 K 维子空间的基向量,通过正交线性变换我们可以将 featrue map 投影到每一个 上,首先是一个将 的正交投影矩阵,经过这个变换矩阵就可以得到特征图在线性子空间的投影
【实验】


从消融实验中可以看到参数量主要还是来源于Blocks
【总结】
UNet在去噪工作里貌似蛮好用的,但是这paper里面 K 也是一个超参数,我原本以为要投影到不同的色彩通道,但是这个子空间也是构造出来的…