【论文阅读·DeepLearning】Deep Residual Learning for Image Recognition

以下解读均为本人个人见解，如有曲解或造成不必要的麻烦，欢迎联系我 nexisato0810@gmail.com 进行修改。正文内容中的“作者”均为paper作者本人，我的观点会由“我”或在括号“()”内显式注明。

【Paper作者】：Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun, 来自微软研究院

【一句话总结】：大名鼎鼎的ResNet

【Introduction】

深度卷积神经网络在图像分类应用上有很大的突破. 通过堆叠更多的层，使得深度神经网络以“端到端”的方式构成了不同层级的特征分类器，网络的深度对于模型学习效果的影响很大. 于是就有这样一个问题：“层数越多的网络，学习效果就越好吗？”

随着深度的增加，一些显著的问题就会暴露出来，最著名的是“梯度消失” 和 “梯度爆炸” 问题，从训练一开始就会阻碍网络的训练. 这两个问题使用 “初始归一化” 和 “中间归一化” 的方法即可在很大程度上得到解决，使得具有数十层神经网络在SGD进行BP优化时可以收敛.

然而，当网络层数加深时，容易发生 “退化(degradation)” 现象：即模型在训练集上的精度达到饱和，随后迅速下降. 这并不是过拟合问题，而且在此时如果要添加更多的网络层数，用于“恒等映射(identity mapping)” （输出直接拟合输入），不仅不会保持浅层网络学习的效果，反而会造成更大的训练误差，如下图所示.

作者提出了一种“深度残差学习框架”用于解决退化问题. 将新堆叠的层用于拟合“残差映射(Residual mapping)”，而非“底层映射（Underlying mapping）”. 如下图Figure 2，我们假设整个 building block的输出为 $\mathcal{H}(x)$ ，表示底层映射；新堆叠的非线性层用于拟合一个 “残差函数” $\mathcal{F}(x) = \mathcal{H}(x) - x$ . 我们作这样一个假设：优化残差映射 $\mathcal{F}(x)$ ，要比优化原始底层映射 $\mathcal{H}(x)$ 要更容易；进而在极端情况下，通过优化得到 $\mathcal{F}(x) = 0$ ，要比通过一堆非线性层优化得到 $H(x) = x$ 更容易.

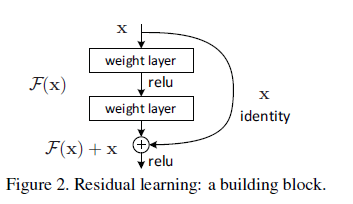
这个残差函数可以通过上图所示的具有“快捷连接(Shortcut connections)”结构的前馈神经网络实现. 快捷连接指的是某层网络的输出，跨过一层或多层神经网络进行连接. 在上图的结构中，快捷连接用于恒等映射，快捷连接的输出被添加到堆叠层的输出中. 这种连接方式，既不会带来额外的参数，又不会增加计算复杂度，网络依然可以通过使用带有BP的SGD优化器进行端到端训练.

作者在ImageNet数据集和CIFAR-10数据集上进行了实验验证，得到如下结论：

深度残差网络易于优化，但是一些“plain”网络（简单地进行堆叠）只是随着网络深度的增加引入了更多的训练误差.
通过大幅度增加网络深度，深度残差网络的识别精度可以得到显著提升.

【深度残差学习】

残差学习

现在回顾一下底层映射 $\mathcal{H}(x)$ ，假设它是由一些堆叠层（并非整个网络）拟合得到的. 其中， $x$ 代表这些堆叠层中第一层的输入，我们让这些非线性堆叠层的输出，去近似拟合残差函数 $\mathcal{F}(x) = \mathcal{H}(x) - x$ ；这样，原始的底层映射函数就可以表示为 $\mathcal{H}(x) = \mathcal{F}(x) + x$ ，两个表达式拟合的难度是不一样的.

如我们在【Introduction】中讨论的那样，如果新堆叠的层用于恒等映射，那么具有更深层网络的模型，训练误差不应该高于浅层网络的训练误差. 但是神经网络的退化问题表明，求解器(特指SGD等)是很难通过多个非线性层去拟合恒等映射的. 因此，我们对这样一个待优化目标函数表达式进行重构，如果恒等映射是最优的，那么求解器就可以在训练中使得非线性层的训练权重逐步逼近为0，从而接近恒等映射.

但是在现实案例中，我们不太可能得到最优恒等映射（多个非线性层为0）. 但是通过我们的残差函数，我们通常会得到很小的响应（学习到的权重很小），从而说明我们这样一个近似的恒等映射可以为模型提供合理的预处理.

通过快捷连接实现恒等映射

我们对每一个堆叠的层都采用残差学习的方法. 在本文中，Figure2所示的building block模型可以表示为

$y = \mathcal{F}(x_i,\{W_i\}) + x$

其中， $x$ 和 $y$ 分别代表building block的输入输出向量，函数 $\mathcal{F}(x_i,\{W_i\})$ 表示这几个堆叠层需要学习的残差映射函数. 如 Figure2中的结构，则该函数就可以表示为 $\mathcal{F} = W_2 \sigma(W_1 x)$ ，其中 $\sigma(·)$ 表示ReLU激活函数和偏置， $\mathcal{F} + x$ 就是经过加入快捷连接得到的输出，并再次经过一个非线性激活层得到输出（即 $\sigma(y)$ ）.

快捷连接不引入额外的参数，也不增大计算复杂度，这是残差网络思想的核心. 我们对 plain network 和 residual network进行对比：假设它们具有同样多的参数、网络深度、宽度和计算代价，设定 $x$ 和 $\mathcal{F}$ 的维度相同（否则进行在快捷连接进行线性投影，对二者的维度进行匹配： $y = \mathcal{F}(x_i,\{W_i\}) + W_sx$ ）).

后续的实验证明，直接连接的恒等映射已经足以解决神经网络的退化问题，因此在实际模型应用中不需要额外引入 $W_s$ ，此处仅仅用于对齐维度.

building blocks实际上可以堆叠多层，但是并不建议只堆叠一层，因为这相当于线性映射 $y = W_1 x + x$ ，作者尚未观察得到一层 building block的优点. 此外，作者目前为止举的例子都在全连接层上，实际上残差学习模型也可应用于卷积层， $\mathcal{F}(x_i,\{W_i\})$ 可以表示多个卷积层，快捷连接的逐元素相加，在卷积层中表现为两个feature map逐channel相加.